calculo: limites

El límite de una función es un concepto fundamental del cálculo diferencial matemático, un caso de límite aplicado a las funciones.

Informalmente, el hecho que una función f tiene un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.

Si f(x) y g(x) son funciones de variable real y k es un escalar, entonces, se cumplen las siguiente propiedades:

Límite de	Expresión
Una constante	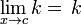$\lim_{x \to c} k =\, k\,$
La función identidad	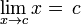$\lim_{x \to c} x = \, c \,$
El producto de una función y una constante	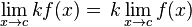$\lim_{x \to c} kf(x) =\, k\lim_{x \to c} f(x)\,$
Una suma	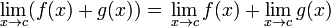$\lim_{x \to c} (f(x) + g(x)) =\, \lim_{x \to c} f(x) + \lim_{x \to c} g(x)\,$
Una resta	$\lim_{x \to c} (f(x) - g(x)) =\, \lim_{x \to c} f(x) - \lim_{x \to c} g(x)\,$
Un producto	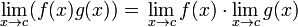$\lim_{x \to c} (f(x) g(x)) =\, \lim_{x \to c} f(x) \cdot \lim_{x \to c} g(x)\,$
Un cociente	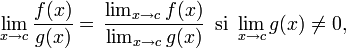$\lim_{x \to c} {{f(x)}\over {g(x)}} =\, {{\lim_{x \to c} {f(x)}} \over {\lim_{x \to c} {g(x)}}}\,\ \mbox{si } \lim_{x \to c} g(x) \ne 0,$
Una potencia	${\lim_{x \to c} f(x)^{g(x)}} =\, {\lim_{x \to c} f(x)^{\lim_{x \to c} g(x)}}\,\ \mbox{si } f(x) > 0$
Un logaritmo	${\lim_{x \to c} \log f(x)} =\, \log {\lim_{x \to c} f(x)}$
El número e	${\lim_{x \to 0} \left(1+x\right)^{1 \over x}} =\, {\lim_{x \to \infty} \left(1+{1 \over x}\right)^x } =\, e$
Función f(x) acotada y g(x) infinitesimal	${\lim_{x \to c} \left(f(x) \cdot g(x)\right)} =\, 0$ .

calculo

lunes, 4 de junio de 2012

limites

No hay comentarios:

Publicar un comentario