derivadas sucesivas

• Al derivar una función puede ocurrir q la
• función resultante sea también derivable,
•  en este caso la derivada de la primera
• derivada se llama la segunda derivada de la
•  función primitiva. Análogamente, la
• derivada de la segunda se llama tercera
• derivada y así sucesivamente.Los símbolos
•  para las derivadas sucesivas se escriben
•  ordinariamente como siguen
• 3. Entonces podemos indicar que los
• símbolos quedarían de la siguiente
• manera:y ’ = 1º Derivaday ’ ’ = 2º Derivaday
•  ’ ’ ’ = 3º Derivaday ’ ’ ’ ’ = 4º Derivada

derivacion de formulas

derivada de una función en un punto

Dada una función y = f(x), se llama derivada de la función f en un punto x0 al 

f'(x0 ) (efe prima de equis sub-cero) o por D(f(x0 )):

Cuando este límite existe (y es finito) se dice que la función f(x) es derivable en el punto x0.

Significado de la derivada

Puesto que

la derivada de la función en un punto x0 no es otra cosa que la pendiente de la tangente a la curva (gráfica de la función) en (x0, f(x0 )).

razon de cambiop por medio de interpretacion geometrica

Comenzando por la Razón Instantánea de Cambio de una función cuya variable independiente es el tiempo t. suponiendo que Q es una cantidad que varía con respecto del tiempo t, escribiendo Q=f(t), siendo el valor de Q en el instante t. Por ejemplo

• El tamaño de una población (peces, ratas, personas, bacterias,…)
• La cantidad de dinero en una cuenta en un banco
• El volumen de un globo mientras se infla
• La distancia t recorrida en un viaje después del comienzo de un viaje

El cambio en Q desde el tiempo t hasta el tiempo t+"t, es el incremento

La Razón de Cambio Promedio de Q (por la unidad de tiempo) es, por definición, la razón de cambio "Q en Q con respecto del cambio "t en t, por lo que es el cociente

Definimos la razón de cambio instantánea de Q (por unidad de tiempo) como el límite de esta razón promedio cuando "t!0. Es decir, la razón de cambio instantánea de Q es

Lo cual simplemente es la derivada f´(t). Así vemos que la razón de cambio instantánea de Q=f(t) es la derivada

La interpretación intuitiva de la razón de cambio instantánea, pensamos que el punto P(t,f(t)) se mueve a lo largo de la gráfica de la función Q=f(t). Cuando Q cambia con el tiempo t, el punto P se mueve a lo largo da la curva. Pero si súbitamente, en el instante t, el punto P comienza a seguir una trayectoria recta, entonces la nueva trayectoria de Pcorresponde que Q cambia a una razón constante.

También como conclusión tenemos que si la pendiente de la recta tangente es positiva ésta es ascendente y si le pendiente es negativa ésta es descendente, así

Q es creciente en el instante t si

Q es decreciente en el instante t si

La derivada de cualquier función, no solamente una función del tiempo, puede interpretarse como una razón de cambio instantánea con respecto de la variable independiente. Si y=f(x), entonces la razón de cambio promedio de y (por un cambio unitario en x) en el intervalo [x,x+"x] es el cociente

La razón de cambio instantánea de y con respecto de x es el límite, cuando "x!0, de la razón de cambio promedio. Así, la razón de cambio instantánea de y con respecto de x es

derivada

Derivada

Consideremos la tangente a la curva f(x) en el punto P(a,f(a)).
¿Cómo se obtiene el ángulo α entre la tangente y el eje x positivo?
El conocimiento de los valores a y f(a) no basta para determinarlo, puesto que hay un número infinito de rectas, aparte de la tangente, que pasan por P.
Tampoco es necesario conocer la función f(x) en su comportamiento global; el conocimiento de la función en una vecindad arbitraria del punto P debe ser suficiente para determinar α. Esto indica que se debería definir la dirección de la tangente a una curva f(x) mediante un proceso de límite.

Consideremos un segundo punto P'(x,f(x)) sobre la curva, cercano a P.
Por los dos puntos P y P' se traza una línea recta.
Si el punto P' se mueve a lo largo de la curva hacia el punto P, entonces la recta PP' se aproxima a la tangente.

Sea α' el ángulo que la recta PP' forma con el eje x positivo.

Entonces lim_P'->P α' = α

Considerando las coordenadas de los puntos P y P', se tiene:

          f(x) - f(a)          cateto opuesto  
tan α' =  -----------       ( ---------------- )
             x - a            cateto adyacente     

Así, nuestro proceso de límite está representado por la ecuación:

                          f(x) - f(a)
tan α = lim tan α' = lim  -----------
        x->a         x->a    x - a

A este límite se lo denomina derivada de la función f(x) en el punto a y se denota f'(a)

Definición

Derivada en el punto a

Se llama derivada de f(x) en x=a, y se denota f'(a) a:

            f(x) - f(a)
f'(a) = lim ----------- 
        x->a   x - a

Función derivada

La derivada es una función de x, puesto que un valor de f'(x) corresponde a cada valor de x.

Teorema

Si una función es derivable, entonces es continua.

H) f es derivable en x=a.
T) f es continua en x=a.

videos sobre limites

http://www.youtube.com/watch?v=Z5_GyMKJTVk

video  realizado por  margarita  velazquez espinoza

http://www.youtube.com/watch?v=wFQGNxDXw&feature=youtu.be

cuntinuidad de una funcion

Continuidad

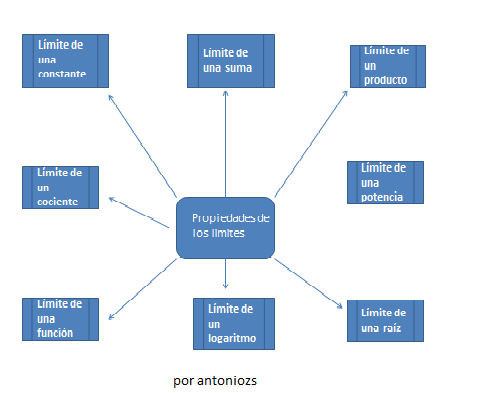
f(x)=x2

Intuitivamente, la continuidad significa que un pequeño cambio en la variable x implica sólo un pequeño cambio en el valor de f(x), es decir, la gráfica consiste de un sólo trozo de curva.

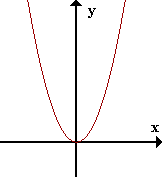
f(x)=sgn x

En contraste, una gráfica como la de la función f(x) = sgn x (signo de x) que consiste de pedazos de curva separados por un vacío en una abcisa exhibe allí una discontinuidad.

La continuidad de la función f(x) para un valor a significa que f(x) difiere arbitrariamente poco del valor f(a) cuando x está suficientemente cerca de a.

Expresemos esto en términos del concepto de límite...

Definición

Continuidad

Una función f(x) es continua en un punto a si lim_x->af(x) = f(a).

Nota: observar que debe existir f(a) y debe existir el lim_x->a f(x) y debe ser igual a f(a).

Ejemplos de discontinuidad

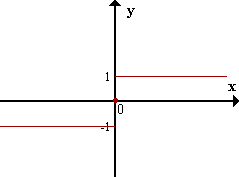
f(x)= 1/x2 Discontinua en x=0 (No existe f(0))

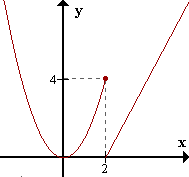f(x) = x2 si x <= 2         2x - 4 si x > 2  Discontinua en x=2. Si bien existe f(2), no existe limx->2f(x), pues limx->2-f(x)=4 y limx->2+f(x)=0

Sin embargo, si miramos la función para x próximos a 2 pero menores, e ignoramos los x mayores que 2, la función es continua en 2 "por la izquierda".

Definición

Continuidad por la izquierda

Una función f(x) es continua por la izquierda en el punto a si existe f(a) y lim_x->a-f(x) = f(a).

Definición

Continuidad por la derecha

Una función f(x) es continua por la derecha en el punto a si existe f(a) y lim_x->a+f(x) = f(a).

La función anterior es continua por la izquierda en x=2, pero no por la derecha.

Definición

Continuidad en un intervalo cerrado [a,b]

Una función f(x) es continua en un intervalo cerrado [a,b] si:
f es continua en a por la derecha
f es continua en b por la izquierda
f es continua en x, para todo x perteneciente al intervalo abierto (a,b)

Clasificación de discontinuidades

Evitable

Caso A:

No existe f(a) pero existe lim_x->af(x).

Ejemplo:

f(x)= e-1/x2 + 2

No existe f(0) pues anula un denominador.

lim_x->0-f(x) = lim_x->0+f(x) = 2 o sea lim_x->0f(x)=2

Podemos extender la definición de la función, asignándole en el punto a el valor del límite, con lo cual la función se torna continua. Por ello este tipo de discontinuidad se denomina evitable.

Caso B:

Existe f(a) y existe lim_x->af(x)=b pero b≠f(a).
(Existe f(a) pero es distinto al valor del límite).

Ejemplo:

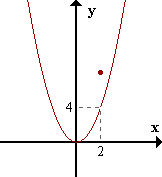f(x) = x2 si x≠2         8 si x=2

f(2) = 8
lim_x->2 f(x) = 4

Asignándole a la función el valor 4 en x=2, se elimina la discontinuidad.

No evitable

1ª especie:

lim_x->a-f(x) ≠ lim_x->a+f(x).
(Los límites laterales son distintos).

Ejemplo:

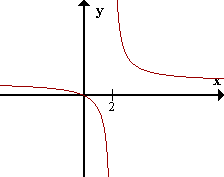f(x) = x/(x - 2)

lim_x->2-f(x) = -inf
lim_x->2+f(x) = +inf

2ª especie:

No existe lim_x->a-f(x) o no existe lim_x->a+f(x).
(No existe por lo menos uno de los límites laterales).

Ejemplo:

______ f(x) = \|x2 - 4

En x=-2 y x=2 la función presenta discontinuidades no evitables de 2ª especie. No existe lim_x->-2+f(x) y no existe lim_x->2-f(x).

Operaciones con funciones continuas

Si f y g son funciones continuas en x=a, la suma, multiplicación y cociente de f y g (con g(a) ≠ 0) son funciones continuas en x=a.

H) f(x) es continua en x=a.
    g(x) es continua en x=a.
T) f(x) + g(x) es continua en x=a.

Demostración

Por definición de continuidad,

existe f(a) y existe lim_x->af(x) = f(a)
existe g(a) y existe lim_x->ag(x) = g(a)

=> por teo. límite de la suma de funciones, el límite de una suma de funciones es igual a la suma de los límites de cada función, si éstos son finitos.

lim_x->a f(x) + g(x) = f(a) + g(a)

=> por def. de continuidad f(x) + g(x) es continua en x=a.

Análogamente se prueba la continuidad del producto y el cociente.

Teorema

Continuidad de la función compuesta

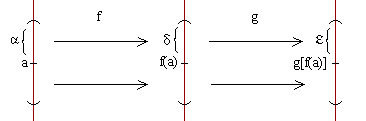
H) f es continua en x=a.
    g es continua en x=f(a).
T) g o f es continua en x=a.

Demostración:

Queremos demostrar que lim_x->a g[f(x)]=g[f(a)], o sea, por definición de límite, queremos probar que, dado ε>0 existe δ>0 tal que para todo x perteneciente al E^*_a,δ g[f(x)] perteneciente al E_g[f(a)],ε.

Por hipótesis g es continua en f(a) => por def. de continuidad lim_x->f(a) g(x)=g[f(a)] => por def. de límite, dado ε>0 existe δ>0 tal que...

para todo x perteneciente al E^*_f(a),δ g(x) pertenece al E_g[f(a)],ε   (1)

Por hipótesis f es continua en a => por def. de continuidad lim_x->af(x) = f(a), es decir que (por def. de límite) si tomamos el número δ de (1), existe α>0 tal que...

para todo x perteneciente al E^*_a,α f(x) pertenece al E_f(a),δ   (2)

De (1) y (2) se deduce que:
Dado ε>0 existe α>0 / para todo x perteneciente al E^*_a,α g[f(x)] pertenece al E_g[f(a)],ε.

propiedades de los limites

El límite de una función en un punto es único. (Se puede decir lo mismo diciendo: Una función no puede tener dos límites diferentes en un mismo punto).

Sean f y g dos funciones. Si el límite de la función f, en el punto x = a, es l, y el límite de la función g, en el punto x = a, es m, entonces el limite de la función f + g, en el punto x = a, es l + m. (Esto se expresa de manera rápida diciendo: El límite de la suma es igual a la suma de los límites).

lim (f(x) + g(x)) = lim f(x) + lim g(x)

Sean f y g dos funciones. Si el límite de la función f, en el punto x = a, es l, y el límite de la función g, en el punto x = a, es m, entonces el limite de la función f * g, en el punto x = a, es l * m. (Esto se expresa de manera rápida diciendo: El límite del producto es igual al producto de los límites).

lim (f(x).g(x)) = lim f(x) . lim g(x)

Sean f y g dos funciones. Si el límite de la función f, en el punto x = a, es l, y el límite de la función g, en el punto x = a, es m (distinto de cero), entonces el limite de la función f / g, en el punto x = a, es l / m. (Esto se expresa de manera rápida diciendo: El límite del cociente es igual al cociente de los límites).

lim (f(x)/g(x)) = lim f(x) / lim g(x)

Sean f y g dos funciones. Si el límite de la función f, en el punto x = a, es l, y el límite de la función g, en el punto x = a, es m, entonces el limite de la función f ^g , en el punto x = a, es l ^m.

lim (f(x))^g(x) = lim (f(x))^{lim g(x)}

Sean f y g dos funciones. Si el límite de la función f, en el punto x = a, es l, y el límite de la función g, en el punto x = a, es m, entonces el limite de la función f(g(x)) (suponiendo que tenga sentido)  en el punto x = a, es l.

limites de una funcion

Límites

Sea f una función. Estamos interesados en el valor de la función f(x) cuando x se aproxima a un valor c, pero no es necesariamente igual a c. Esto es, ¿según x se aproxima más y más a c (pero x no es igual a c) se acerca f(x) más y más a un valor L? Si la respuesta es si, decimos que "f(x) tiende a L según x se aproxima a c", y se representa en forma simbólica de la forma:

La frase "x se aproxima a c" o "x tiende a c" significa que independientemente de lo próximo que esté x del valor c , existe siempre otro valor de x (distinto de c) en el dominio de f está aún más próximo a c .

Una función no puede tender a dos límites distintos a la vez. Esto es, si el límite de una función existe, es único.

Teorema: El límite,

existe si el límite por la izquierda,

y el límite por la derecha,

son iguales.

Propiedades de límites:  Sean n un entero positivo, k una constante y f,g funciones que tengan límites en c.  Entonces: